leetcode 307. 区域和检索 - 数组可修改

发表于 | 分类于

给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。

示例:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

说明:

  • 数组仅可以在 update 函数下进行修改。
  • 你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。

正常的思路容易想到每次求和的时间复杂度为O(n)， 更新数组元素的时间复杂度为O(1), 因此总体的时间复杂度为 O(n)。但是通过使用segment tree可以将求和以及更新数组元素操作的时间复杂度均变为 O(log2n)。

Segment Tree是一棵二叉树，其特点为叶子节点个数与数组的长度相同 从左到右依次为数组中下标从小到大的元素的值，父节点的值为其左右的叶子节点的值的和。如下图是一个简单的例子

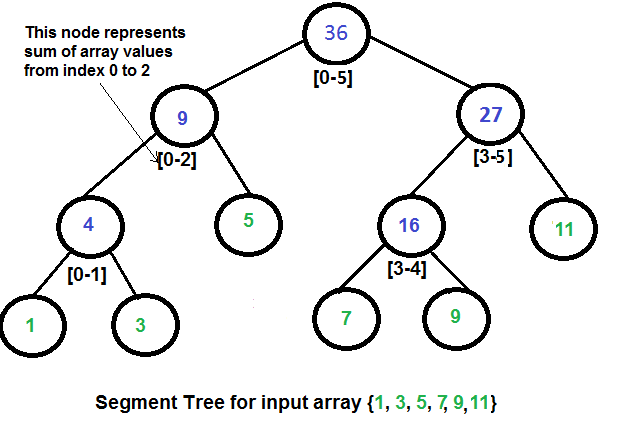
因此可以看到每个非叶子节点的值均是代表了数组某个区间的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class NumArray(object):
    def __init__(self, nums):
        """
        initialize your data structure here.
        :type nums: List[int]
        """
        n = len(nums)
        if n == 0: return
        max_size = 2 * pow(2, int(math.ceil(math.log(n, 2)))) - 1
        self.seg_tree = [0 for i in xrange(max_size)]
        self.nums = nums[:]
        self.build_tree(0, n-1, 0)
        
    def build_tree(self, start, end, curr):#构造segment tree
        if start > end: return # empty list
        if start == end:
            self.seg_tree[curr] = self.nums[start]
        else:
            mid = start + (end - start)/2
            self.seg_tree[curr] = self.build_tree(start, mid, curr*2+1) + self.build_tree(mid+1, end, curr*2+2)
        return self.seg_tree[curr]        
        
    def update(self, i, val):
        """
        :type i: int
        :type val: int
        :rtype: int
        """
        diff = val - self.nums[i]
        self.nums[i] = val
        self.update_sum(0, len(self.nums)-1, i, 0, diff)
    
    def update_sum(self, start, end, idx, curr, diff):#更新segment tree某个元素的值
        self.seg_tree[curr] += diff
        if start == end: return
        mid = start + (end - start)/2
        if start <= idx <= mid:
            self.update_sum(start, mid, idx, curr*2+1, diff)
        else:
            self.update_sum(mid+1, end, idx, curr*2+2, diff)
        
    def sumRange(self, i, j):
        """
        sum of elements nums[i..j], inclusive.
        :type i: int
        :type j: int
        :rtype: int
        """
        return self.get_sum(0, len(self.nums)-1, i, j, 0)
        
    def get_sum(self, start, end, qstart, qend, curr):#segment tree特定区间求和
        mid = start + (end - start)/2
        if qstart > end or qend < start:
            return 0
        elif start >= qstart and end <= qend:
            return self.seg_tree[curr]
        else:
            return self.get_sum(start, mid, qstart, qend, curr*2+1) + self.get_sum(mid+1, end, qstart, qend, curr*2+2)