leetcode 304. 二维区域和检索 - 矩阵不可变

发表于 | 分类于

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。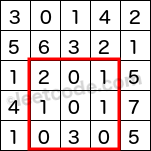
sd
Range Sum Query 2D
上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

说明:

  • 你可以假设矩阵不可变。
  • 会多次调用 sumRegion 方法。
  • 你可以假设 row1 ≤ row2 且 col1 ≤ col2。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class NumMatrix(object):

    def __init__(self, matrix):
        """
        :type matrix: List[List[int]]
        """
        if not matrix or not matrix[0]:
            self.matrix = None
            return
        self.rows = len(matrix)
        self.cols = len(matrix[0])
        self.matrix = matrix
        self.SM = [[0]*self.cols for _ in range(self.rows)]
        self.update()
        
    def update(self):
        if self.rows > 0 and self.cols > 0:self.SM[0][0] = self.matrix[0][0]
        for i in range(1,self.rows):
            self.SM[i][0] = self.SM[i-1][0] + self.matrix[i][0] 
        for j in range(1,self.cols):
            self.SM[0][j] = self.SM[0][j-1] + self.matrix[0][j]
        for i in range(1,self.rows):
            for j in range(1,self.cols):
                self.SM[i][j] = self.SM[i-1][j] + self.SM[i][j-1] - self.SM[i-1][j-1] + self.matrix[i][j]
            
    def sumRegion(self, row1, col1, row2, col2):
        if self.matrix == None or (self.rows == self.cols and self.rows == 0) or row1<0 or row1>=self.rows or row2<0 or row2>=self.rows or col1<0 or col1>=self.cols or col2<0 or col2>=self.cols:return 0
        up = self.SM[row1-1][col2] if row1 >= 1 else 0
        diag = self.SM[row1-1][col1-1] if row1 >= 1 and col1 >= 1 else 0
        left = self.SM[row2][col1-1] if col1 >= 1 else 0
        return self.SM[row2][col2]- up - left + diag


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)